题解 BZOJ2238 Mst

发表于 | 更新于

$Description$

给出一个$N$个点$M$条边的无向带权图，以及$Q$个询问，每次询问在图中删掉一条边后图的最小生成树。(各询问间独立，每次询问不对之后的询问产生影响，即被删掉的边在下一条询问中依然存在)

$Solution$

我们先做好图的最小生成树。

如果删除的边不在最小生成树上，那答案就是最小生成树，直接输出即可。

此时要找能够代替删去的边的一条权值最小的边。用这条边代替删去的边后就是新的最小生成树了。

那怎么代替呢？

我们把最小生成树的样子画个图看看

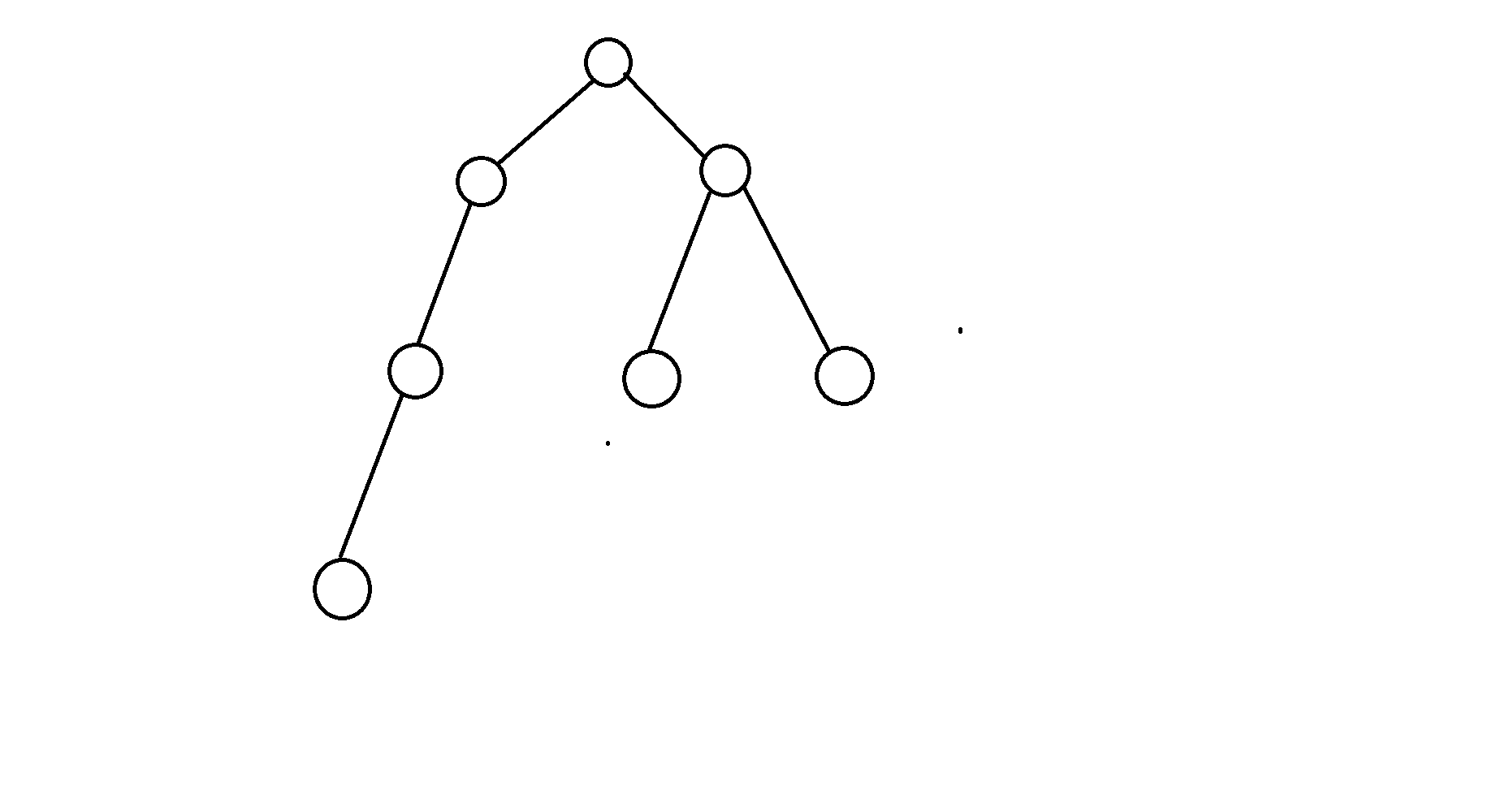
再删去一条边

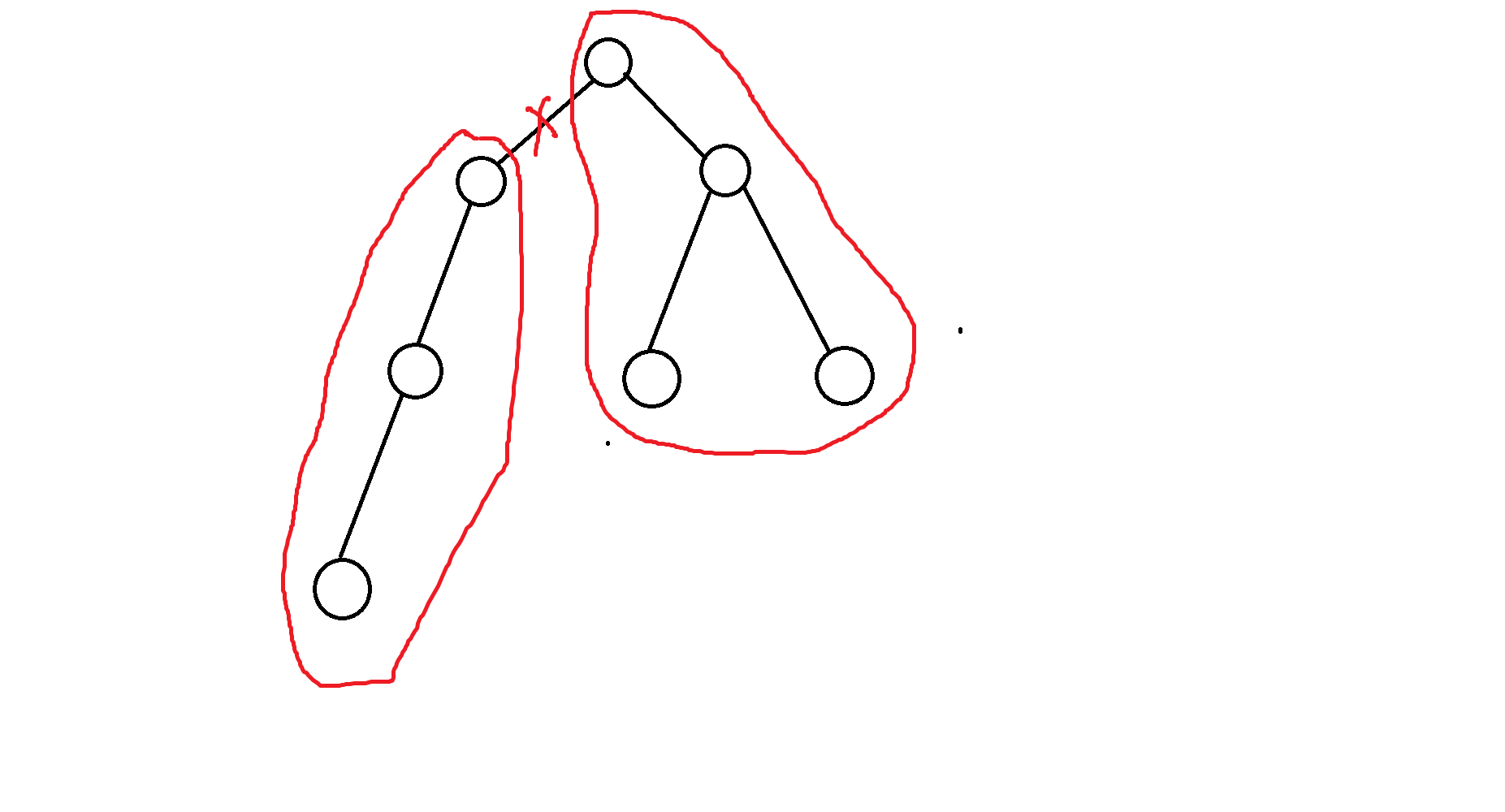
是不是就变成了两个部分

我们要找的就是所有能使两个连通块连通的非树边。这样的非树边就能够代替删去的边重新使树连通。

那怎么找一条权值最小的边$?$

现在反过来想，一条非树边可以代替哪些边$?$

一条非树边可以代替其两端点在树上的简单路径之间的所有边

画一下图即可，如果删去边不在简单路径上，那么删去边的两端一定在同一个部分(即无法在异侧)

然后对于每条非树边，用它的值去更新它两端点构成的简单路径上的边，用树链剖分优化复杂度

先预处理出最小生成树，然后将这棵最小生成树进行树链剖分，每一条边记录能够代替它的、权值最小的非树边的长度。对于每条非树边，利用树剖更新其两端点在树上的简单路径之间的所有边记录的最小值。查询时直接查询删除的边上存储的最小值即可。

实际代码可以将边的信息存在其儿子节点上，简化代码复杂度

有两种情况要特判$Not connected:$

原图不连通，对于所有询问都输出$Not connected($树链剖分只是维护用其它边替换一条边的情况，如果原图不连通的话，不但生成树会建错，而且替换了边树也不连通$);$

原图连通，但删去这条边后没有边能替它连通两个块，此时树链剖分上询问这条边所得到的值应该是没更新过的初值，即$inf$。因此判断这个询问值如果是$inf$就输出$Not connected$即可。

还有一些细节代码中有注释

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
#include <bits/stdc++.h>
#define ll long long
#define re register
#define inf 0x3f3f3f3f
#define ls(k) (k<<1)
#define rs(k) (k<<1|1)
#define N 1000600
using namespace std;
struct node{
    int u,v,d,id;
}p[N];
struct edge{
    int to,next;
}e[N];
inline int read(){
    int x=0,w=0;char ch=getchar();
    while (!isdigit(ch))w|=ch=='-',ch=getchar();
    while (isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
    return w?-x:x;
}
int n,m;
int f[N],vis[N],num[N];
int cnt,head[N];
int mn[N],tag[N];
int size[N],fa[N],top[N],son[N],dep[N],id[N],a[N],tot;
int find(int k){
    return f[k]==k?k:f[k]=find(f[k]);
}
inline void Add(int u,int v){
    e[++cnt].to=v;
    e[cnt].next=head[u];
    head[u]=cnt;
}
inline bool cmp(node a,node b){
    return a.d<b.d;
}
inline void pushup(int k){
    mn[k]=min(mn[ls(k)],mn[rs(k)]); 
}
void add(int k,int d){
    tag[k]=min(tag[k],d);
    mn[k]=min(mn[k],d);
}
void pushdown(int k){
    add(ls(k),tag[k]);
    add(rs(k),tag[k]);
    tag[k]=inf;
}
void build(int k,int l,int r){
    tag[k]=mn[k]=inf;
    if (l==r)
        return;
    int mid=l+r>>1;
    build(ls(k),l,mid);
    build(rs(k),mid+1,r);
}
void change(int k,int l,int r,int x,int y,int d){
    if (x<=l&&r<=y){
        add(k,d);
        return;
    }
    int mid=l+r>>1;
    if (tag[k]!=inf)pushdown(k);
    if (x<=mid)change(ls(k),l,mid,x,y,d);
    if (mid<y) change(rs(k),mid+1,r,x,y,d);
    pushup(k);
}
int query(int k,int l,int r,int x,int y){
    if (x<=l&&r<=y)
        return mn[k];
    int mid=l+r>>1,res=inf;
    if (tag[k]!=inf)pushdown(k);
    if (x<=mid)res=min(res,query(ls(k),l,mid,x,y));
    if (mid<y) res=min(res,query(rs(k),mid+1,r,x,y));
    return res;
}
int Kr(){
    for (int i=1;i<=n;++i)f[i]=i;
    int res=0,cnt=0;
    for (int i=1;i<=m&&cnt<n-1;++i){
        int x=find(p[i].u),y=find(p[i].v);
        if (x==y)continue;
        f[x]=y;
        Add(p[i].u,p[i].v);
        Add(p[i].v,p[i].u);
        ++cnt;res+=p[i].d;vis[p[i].id]=1;
    }
    if (cnt!=n-1)return -1;
    return res;
}
void dfs1(int u){
    size[u]=1;
    for (int i=head[u];i;i=e[i].next){
        int v=e[i].to;
        if (v==fa[u])continue;
        dep[v]=dep[u]+1;fa[v]=u;
        dfs1(v);
        size[u]+=size[v];
        if (!son[u]||size[v]>size[son[u]])son[u]=v;
    }
}
void dfs2(int u,int tp){
    top[u]=tp;
    id[u]=++tot;
    a[tot]=u;
    if (son[u])dfs2(son[u],tp);
    for (int i=head[u];i;i=e[i].next){
        int v=e[i].to;
        if (v==fa[u]||v==son[u])continue;
        dfs2(v,v);
    }
}
void updata(int x,int y,int d){
    while (top[x]!=top[y]){
        if (dep[top[x]]<dep[top[y]])swap(x,y);
        change(1,1,n,id[top[x]],id[x],d);
        x=fa[top[x]];
    }
    if (dep[x]>dep[y])swap(x,y);
    change(1,1,n,id[x]+1,id[y],d);//当前的x即使原先x,y两点的lca，由于边的权值存在子节点上，所以lca是不能取的 
}
int query1(int x,int y){
    int res=inf;
    while (top[x]!=top[y]){
        if (dep[top[x]]<dep[top[y]])swap(x,y);
        res=min(res,query(1,1,n,id[top[x]],id[x]));
        x=fa[top[x]];
    }
    if (dep[x]>dep[y])swap(x,y);
    return min(res,query(1,1,n,id[x]+1,id[y]));
}
signed main(){
    n=read(),m=read();
    for (int i=1;i<=m;++i)p[i].u=read(),p[i].v=read(),p[i].d=read(),p[i].id=i;
    int q=read();
    sort(p+1,p+1+m,cmp);
    for (int i=1;i<=m;++i)num[p[i].id]=i;
    int res=Kr();
    if (res==-1){while (q--){puts("Not connected");}return 0;}
    dfs1(1);dfs2(1,1);
    build(1,1,n);
    for (int i=1;i<=m;++i)
        if (!vis[p[i].id])
            updata(p[i].u,p[i].v,p[i].d);
    while (q--){
        int k=read();
        if (!vis[k]){printf("%d\n",res);continue;}
        int ans=query1(p[num[k]].u,p[num[k]].v);
        if (ans==inf)puts("Not connected");
        else printf("%d\n",res-p[num[k]].d+ans);
    }
    return 0;
}